Position du problème
Contexte de comparaison de deux moyennes observées
On souhaite comparer deux groupes (malade ou pas, ville A - Ville B, etc) sur un critère quantitatif (cholestérolémie, salaire, etc).
On constitue au préalable deux groupes en tirant au sort un échantillon dans chaque groupe
On mesure les données à comparer sur chaque sujets dans chaque groupe
La comparaison suppose l'utilisation d'un test statistique qui va comparer les moyennes des deux groupes, test qui permettra de savoir si un groupe a une moyenne différente de l'autre groupe, en tenant compte de la variabilité des données.
D'où les hypothèses
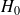et
:
-
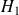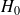: les deux moyennes ne diffèrent pas :
-
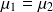
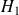: les moyennes diffèrent :
Remarque :
Les variances
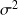n'interviennent pas dans la formulation des hypothèses alors qu'elles sont indispensables pour réaliser le test.
Une hypothèse très forte nécessaire pour comparer les moyennes est que les variances sont égales dans les deux populations = homoscédasticité des variances.
Dans ce cours on admettra toujours que les variances ne sont pas différentes, mais dans la vraie vie il faut le vérifier (cette vérification est hors cours).
Pourquoi ? Car cela permet de dire que l'effet du facteur se manifeste par un décalage des valeurs et pas par un décalage plus une dilatation des valeurs. Si le traitement modifiait les moyennes et les variances, on testerait deux choses simultanément sans que l'on puisse les distinguer par ce test.
On compare donc des moyennes et pas un décalage entre les deux ensembles de valeurs.
