Statistiques de base

1. Définition

Notre maison médicale voudrait s'agrandir avec un nouveau médecin avec une formation avancée en gynécologie. Il souhaiterait avoir une idée du potentiel d'une nouvelle patientelle féminine. Pour cela nous avons analysé les patients venu consulter sans rendez-vous. Sur une journée de travail, un médecin reçoit en moyenne 15 patients sans rendez-vous soit environ 45 patients sur l'ensemble des 3 médecins. Quel est parmi ces patients le nombre de femmes ?

Nous faisons les 3 hypothèses suivantes :

1. Il est impossible de prévoir le sexe du prochain patient : expérience aléatoire

2. Il n'y a aucune relation entre la venue d'un patient, celui qui l'a précédé et le suivant : indépendance des évènements.

3. Quel que soit le patient, il pourra toujours être classé de la même manière soit comme un homme ou une femme.

Soit X la VA qui décrit le nombre de femme pouvant être reçu en consultation sans rendez-vous sur une journée dans la maison médicale.

Soit p la probabilité d'observer une femme pour un patient donné.

La distribution de probabilité de la VA est donnée par la fonction distribution binomiale définit de la manière suivante :

Où : n=nombre de réalisation de l'expérience aléatoire et s=nombre de succès

La distribution binomiale dépend de 2 paramètres n et p. Elle est noté B(n,p).

2. Caractéristiques

3. Pratique

Les formules Excel suivante permette de construire les tables de probabilité et les tables de probabilité commune pour une loi binomiale :

Tableau

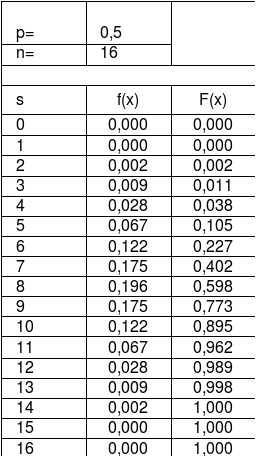
4. La table de la loi binomiale

Comme la majorité des tables des lois statistiques, elles fournissent en fonction de certains paramètres, les probabilités cumulées. Pour la loi binomiale les paramètres requis sont les suivantes :

• La probabilité du succès ou de l'évènement élémentaire étudié. Pour l'exemple c'était la probabilité qu'un patient soit une femme.

• Le nombre de succès

• Le nombre total de réalisation de l'expérience