B. Loi normale
1. Définition
La distribution normale est la distribution la plus importante en statistique. Un grand nombre d'autres distribution comme celle binomiale peut-être approchée par une distribution normale d'où l'intérêt de son étude. Aussi appelée distribution de de Laplace Gauss, elle est utilisée pour décrire exclusivement des variables aléatoires continues. Sa fonction densité de probabilité dépend de 2 paramètres notés habituellement par les lettres grecques µ et σ qui sont des nombres réels avec σ>0. Elle est notée N(µ ;σ) et définie par :
![]()
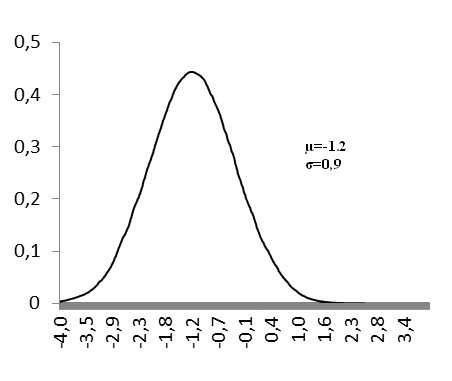
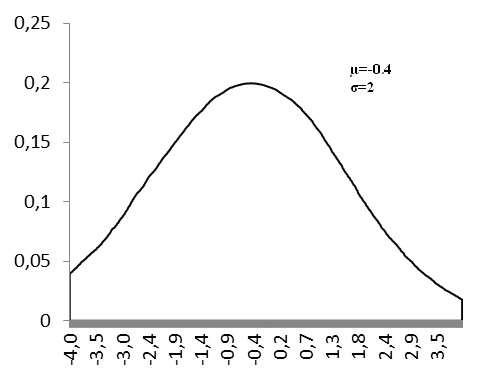
Les 2 figures ci-dessous montrent 2 représentation graphiques de N(-1,2 ;0,9) et N(-0,4 ;2)
2. Caractéristiques

Contrairement aux distributions pour les VA discrète où il est possible de déterminer la probabilité pour un événement élémentaire, dans le cas continue cette valeur est nulle.
Le calcul de la probabilité d'événement quelconque fait appel à un calcul d'intégral. En effet, si X est une VA continue la probabilité d'un événement [a,b], autrement dit la probabilité d'observer un élément x de X(Ω) qui soit compris dans l'intervalle [a,b] est donnée par la formule :
![]()
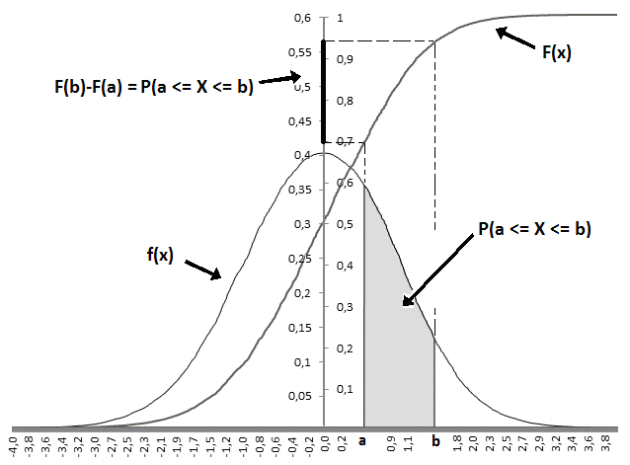
Cette probabilité peut se calculer de deux manières comme le montre la figure 3 ci-dessous :
Soit comme l'aire sous la courbe de la fonction densité de probabilité (zone en gris sur la figure)
Soit à partir de la fonction de répartition par la différence de F(b) et F(a) qui est figurée sur la figure par un trait en gras sur l'axe vertical.
Il s'agissait d'un calcul fastidieux et c'est pourquoi des tables de statistiques ont été construites et qui permettent de retrouver soit les valeurs de a et b, soit les probabilités correspondantes.
3. La loi normale centrée réduite
Soit X une VA admettant pour espérance mathématique ou moyenne µ et pour écart-type σ.
On dit que l'on centre X si on considère l'écart à sa moyenne et qu'on la réduit si on considère le rapport à son écart-type.
Soit une variable Z telle que![]() on dit que Z représente la variable centrée réduite X.
on dit que Z représente la variable centrée réduite X.
Z est une VA qui peut prendre toutes valeur positive ou négative et qui a pour moyenne et écart-type : ![]()
La loi normale centrée réduite correspond à la loi normale avec pour paramètre µ = 0 et σ = 1 (N(0 ;1). Sa fonction densité de probabilité est symétrique par rapport à sa moyenne (voir figure 3). C'est cette fonction que l'on retrouve représentée dans les table statistique pour la distribution normale et ceci pour les raisons suivantes :
La symétrique permet de ne construire les tables que pour les valeurs positives
Ainsi,
![]()
Tout loi normale N(µ ;σ) peut être ramenée à une loi normale N(0 ;1) par les opérations successives de centrage et de réduction de la VA.
Ainsi,
![]()
4. Tables de la loi normale
Nous allons considérer la VA X centrée réduite de telle sorte que ![]()
Vous trouverez deux types de tables :
La table de f(z)
Cette table permet de lire la probabilité P(Z≤z) c'est-à-dire d'observer des valeurs de X inférieures à µ+z*σ.
.gif)
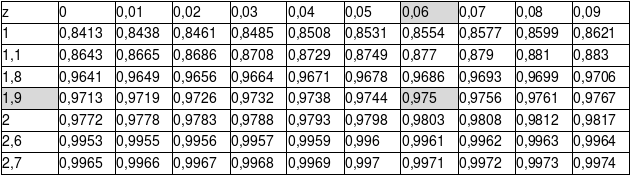
Exemple :
Soit à déterminer P(Z≤1,96)= ?
On construit la valeur 1,96 en additionnant les valeurs de la première colonne et de la première ligne
On lit ensuite la valeur au croisement de la ligne et de la colonne correspondante
Ainsi P(Z≤1.96)= 0.9750 (voir les zone grisée sur l'extrait de la table ci-dessus)
Grâce à la symétrie, on déduit que P(Z≤-1,96)= 1-P(Z≤-1,96)=0,0250
La table de l'écart-réduit
Par rapport à la table précédente, ici on connaït la probabilité notée α et nous cherchons à déterminer la valeur de z telle que P(-z≤Z≤z) = P(|Z|≤z) =1- α.
Autrement dit, α représente la probabilité d'être à l'extérieur de l'intervalle délimité par –z et z.
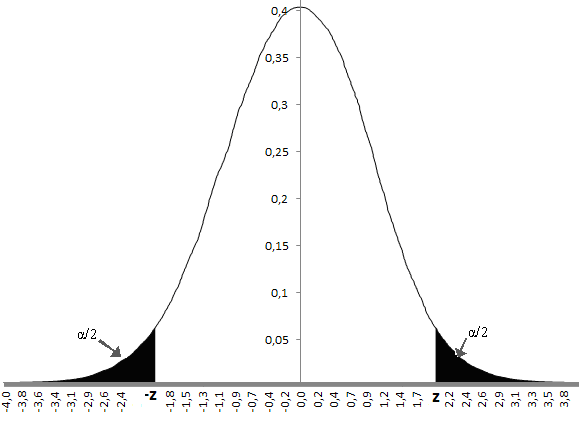

Exemple :
Soit à déterminer P(|Z|≤ ?)= 0,05. Ici α=0,05
On construit la valeur 0,05 en additionnant les valeurs de la première colonne et de la première ligne
On lit ensuite la valeur au croisement de la ligne et de la colonne correspondante
Ainsi P(Z≤1,96)= 0,05 c'est-à-dire que la probabilité d'obtenir une valeur qui se trouve à l'extérieur de l'intervalle [-1,96 ; 1,96] est de 5%.