Cas des variables quantitatives
Présentation du jeu de données
Nous allons travailler sur la série de données suivante qui représente 200 mesures de la taille des patients admis dans un hôpital. La variable aléatoire quantitative continue sera notée X.

Nous allons distinguer 3 groupes de paramètres :
Les paramètres de tendances centrales
La médiane
C'est la valeur de la variable qui divise la série de données en 2 parties de telle sorte qu'une moitié des valeurs lui sont inférieures et l'autre lui sont supérieures.
Exemple :
La médiane de X est 152 cm
La moyenne
Nous parlerons dans ce cours uniquement de la moyenne arithmétique. C'est le rapport entre la somme de l'ensemble des valeurs observées sur le nombre total d'unités statistiques.
Soit X une variable quantitative mesurée sur N d'individus. Soient x1, x2, ..., xN les valeurs observées.
observées. La moyenne de X notée m ou
est donnée par la formule suivante :
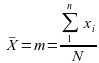
Exemple :
La moyenne de X est 151,5 cm
Les paramètres de position
Le premier quartile (Q1)
C'est la valeur de la variable qui divise l'ensemble de la distribution en 2 parties de telle manière que l'ensemble des valeurs qui lui sont inférieures représente 25% de la distribution. On peut aussi la définir comme la plus grande des 25% plus petites valeurs de la distribution. On le note souvent Q1.
Exemple :
Q1= 143 cm
Le deuxième quartile (Q2)
Il s'agit de la médiane que nous avons définie plus haut.
Le troisième quartile (Q3)
C'est la valeur de la variable qui divise l'ensemble de la distribution en 2 parties de telle manière que l'ensemble des valeurs qui lui sont supérieures représente 25% de la distribution. On peut aussi la définir comme la plus petite des 25% plus grandes valeurs de la distribution. On le note souvent Q3.
Exemple :
Q3= 159 cm
Les paramètres de dispersion
Étendu interquartile
C'est la différence entre Q3 et Q1. Il s'agit d'une mesure de la dispersion qui concerne 50% des valeurs les plus fréquentes en neutralisant les valeurs extrême inhabituelles. Elle indique l'écart maximum entre les valeurs constituant 50% de la distribution.
Exemple :
L'étendu interquartile = 16 cm
La variance et l'écart-type
La variance est la somme des carrés des écarts à la moyenne divisé par le nombre d'observation.
Si nous reprenons les notations utilisées dans la définition de la moyenne ci-dessus la variance est donnée par la formule suivante :
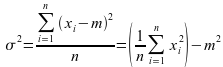
Remarque :
NB : Quand on veut estimer la variance d'une variable X à partir d'un échantillon (une partie de la population sélectionnée au hasard) de taille n on utilise la variance « corrigée » divisée par n-1 que l'on note Sx2.
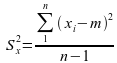
Exemple :
variance = 168,32 cm2 écart-type=12,97 cm
Coefficient de variation (CV)
Le coefficient de variation est le rapport de l'écart-type à la moyenne exprimé en pourcentage. C'est un nombre sans dimension qui permet de comparer la variabilité de phénomènes mesurés avec différentes unités
Exemple :
CV =9%





