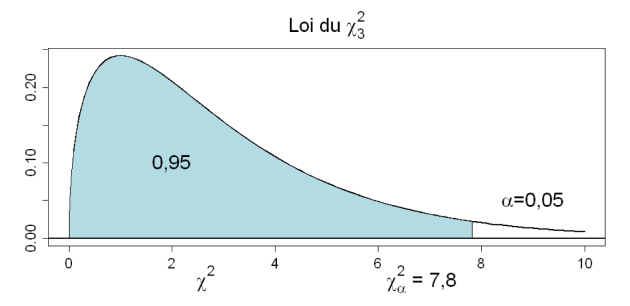
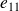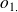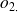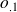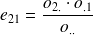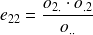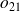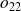Construction du test
On souhaite comparer deux proportions observées
les effectifs observés subissent des fluctuations d'échantillonnage
sous
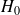 la répartition des effectifs en lignes est identique d'une colonne à l'autre et vice-versa.
la répartition des effectifs en lignes est identique d'une colonne à l'autre et vice-versa.Par exemple, sous égalité parfaite (
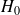 ) on observe :
) on observe :
Exemple :
Col.1 | Col.2 | Total | |
Ligne 1 | 10 | 10 | 20 |
Ligne 2 | 84 | 842 | 168 |
Total | 94 | 94 | 188 |
Dans cet exemple :
la répartition en colonne est la même d'une ligne à l'autre
la répartition en ligne est la même d'une colonne à l'autre
Attention :
L'égalité des répartitions en ligne et en colonnes est une égalité en proportion et pas en effectifs ! Par exemple :
Col.1 | Col.2 | Total | |
Ligne 1 | 10 | 5 | 15 |
Ligne 2 | 84 | 42 | 126 |
Total | 94 | 47 | 141 |
Col.1 | Col.2 | Col.3 |
0,106 | 0,106 | 0,106 |
0,894 | 0,894 | 0,894 |
1 | 1 | 1 |
Col.1 | Col.2 | Total |
0,667 | 0,333 | 1 |
0,667 | 0,333 | 1 |
Sous
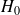 : égalité des répartitions en lignes / colonnes
: égalité des répartitions en lignes / colonnes
Les effectifs observés sont tels que les proportions diffèrent numériquement
le test suppose la comparaison des effectifs observés et des effectifs sous
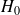
comment obtenir les effectifs sous
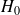 , i.e. effectifs théoriques (attendus) sous
, i.e. effectifs théoriques (attendus) sous
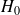 ?
?
Comment obtenir les effectifs théoriques ?
en l'absence de différence de répartitions entre lignes / entre colonnes, les meilleures estimations des proportions de succès / échec sont obtenues à partir des effectifs marginaux.
s'il n'y a pas de différence entre les groupes, les répartitions en lignes / colonnes sont en moyenne identiques entre elles et identiques à la distribution marginale ligne/colonne
Groupe 1
Groupe 2
Total
Modalité 1
10
5
15
Modalité 2
84
42
126
Total
94
47
141
sous
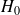 , les répartitions marginales doivent être identiques pour chaque ligne/colonne
, les répartitions marginales doivent être identiques pour chaque ligne/colonnedonc l'effectif théorique d'une cellule sous
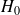 est la valeur attendue sous
est la valeur attendue sous
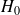
les valeurs attendues obtenues sous
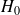 sont estimées à partir du produit des marges
sont estimées à partir du produit des margessoit une répartition de chaque ligne/colonne au prorata de chaque colonne/ligne
Remarque :
Soit sur un tableau :
G 1 | G 2 | total | |
Modalité 1 |
|
| |
Modalité 2 |
| ||
Total |
|
|
|
sous
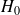 :
:

de façon générale :

Remarque :
Soit sur un tableau à 4 cases :
G 1 | G 2 | Total | |
Modalité 1 |
|
|
|
Modalité 2 |
|
|
|
Total |
|
|
|
Remarque :
On se retrouve avec 2 tableaux !
G 1 | G 2 | total | |
Modalité 1 |
|
|
|
Modalité 2 |
|
|
|
Total |
|
|
|
G 1 | G 2 | total | |
Modalité 1 |
|
|
|
Modalité 2 |
|
|
|
Total |
|
|
|
 un tableau de valeurs observées et un tableau de valeurs théoriques ou attendues sous
un tableau de valeurs observées et un tableau de valeurs théoriques ou attendues sous
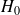
Le problème de la comparaison de deux proportions devient le problème de la comparaison de deux répartitions
qui se ramène à la comparaison de deux tableaux : l'un observé et l'autre théorique
Comment calculer l'écart entre ces deux tableaux ?
dans une cellule
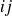 , « distance » entre effectif observé
, « distance » entre effectif observé
 et effectif théorique
et effectif théorique
 :
:
cette distance par cellule est sommée sur l'ensemble des cellules :
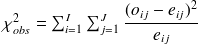
on montre que
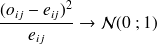
or une somme de

Attention : Test du X²
La comparaison de la répartition des lignes et des colonnes d'un tableau se fait par un test du
 à k ddl.
à k ddl.
Synthèse : la logique du test
En l'absence de différence de répartition (i.e. absence de différence de proportions), les valeurs observées sont égales aux valeurs théoriques sur l'ensemble des cellules
Donc, sous
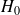 :
:
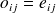 ,
,
 et
et
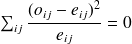
Si
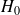 est fausse :
est fausse :les écarts sont d'autant plus importants que les distributions diffèrent et donc :
plus les proportions / répartitions diffèrent
plus les écarts
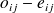 augmentent
augmententplus la valeur de
 augmente
augmente
La valeur du
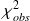 sera comparée à une valeur seuil
sera comparée à une valeur seuil

Les hypothèses du test
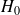 : les répartitions en lignes / en colonnes ne diffèrent pas
: les répartitions en lignes / en colonnes ne diffèrent pas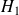 : les répartitions en lignes / en colonnes diffèrent
: les répartitions en lignes / en colonnes diffèrent
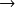 formulation générale, à adapter à chaque cas
formulation générale, à adapter à chaque cas
La procédure
remplir le tableau de contingence
calculer le nombre de degrés de liberté
calculer les effectifs théoriques
calculer la valeur du
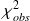
si
 : on rejette
: on rejette
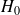
sinon, on ne rejette pas
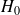
Remarque :
(1) Conditions d'application du test du
 : tous les
: tous les

(2) dans le cas d'une table
 , {i.e.} cas de la comparaison de deux proportions :
, {i.e.} cas de la comparaison de deux proportions :
le test
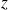 et le test du
et le test du
 sont strictements équivalents car
sont strictements équivalents car