Tableau de contingence : Définition et description
Le tableau 1 ci-dessus est un exemple de tableau de contingence. Il s'agit d'un tableau statistique qui permet de présenter simultanément et de manière croisée 2 séries statistiques.
Dans le chapitre précédent, les séries de données individuelles étaient analysées. Dans ce chapitre nous travaillerons sur des tableaux de contingences, soit 2 séries à la fois.
Les méthodes décrites dans le cadre de la description des séries de données individuelles vont être étendues aux tableaux de contingence. Il s'agit notamment du calcul des effectifs et des fréquences. En plus nous aborderons un problème pratique qui est la notion d'indépendance entre les variables représentées dans le tableau de contingence.
Effectifs
Soit X la VA dont les modalités sont présentées en ligne (Taille) et I le nombre total de ses modalités (I=4).
Soit Y la VA dont les modalités sont présentées en colonne (VerreAlcool) et J le nombre total de ses modalités (J=3).
i désigne l'indice d'une ligne. xi est une modalité de X avec i=0,...,I-1
j désigne l'indice d'une colonne. yj est une modalité de Y avec j=0,...,J-1
nij désigne l'effectif partiel. C'est la valeur que l'on trouve lorsque l'on croise sur le tableau une modalité en ligne (xi) et une modalité en colonne (yj). Elle s'interprète comme étant le nombre d'individus présentant simultanément la modalité xi et la modalité yj
Exemple : à partir du tableau1,
n21 = 124 qui s'interprète comme étant le nombre de personnes interrogées qui avaient une taille mesurée comprise entre 1m75 et 1m84 et disaient avoir consommées entre 3 et 7 verres d'alcool pendant la soirée.
ni désigne l'effectif marginal de X. Il s'agit de l'effectif total en ligne.
n.j désigne l'effectif marginal de Y. Il s'agit de l'effectif total en colonne.
Exemple :
n2. = 255 qui s'interprète comme étant le nombre total de personnes interrogées ayant une taille mesurée entre 1m75 et 1m84
n.1 = 447 qui s'interprète comme étant le nombre de personnes interrogées qui disaient avoir consommés entre 3 et 7 verres d'alcool pendant la soirée.
N = n.. correspond à l'effectif total.
Exemple : N=861
Les formules permettant de déduire ces effectifs sont résumées ainsi :
Soit i=0,1, ..., I-1 et j=0,1, ..., J-1
Vous pouvez vérifier le calcul des effectifs marginaux sur le tableau 1.
Les fréquences
fij désigne une fréquence partielle. C'est-à-dire le rapport entre un effectif partiel (nij) et l'effectif total (N). Autrement dit, il s'agit de la proportion de la fréquence relative de chaque cellule.
Exemple :
Dans le tableau2 ci-dessous, les effectifs partiels issus du tableau1 ont été remplacés par les fréquences partielles
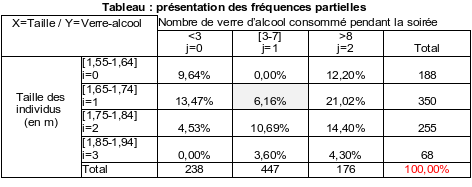
Dans la cellule grisée, nous pouvons lire que les individus mesurant entre 1m65 et 1m74 et ayant consommée entre 3 et 7 verres d'alcool durant la soirée représente 6,16% (f11) des individus interrogés (861).
NB : la somme de tous les fij doit être égale à 100%
fi. désigne la fréquence marginale de X. C'est la fréquence totale en ligne.
f.j désigne la fréquence marginale de Y. C'est la fréquence totale en colonne.
Les formules permettant de déduire ces fréquences sont résumées ainsi :
Soit i=0,1, ..., I-1 et j=0,1, ..., J-1
Exemple :
Dans le tableau3 ci-dessous, les effectifs marginaux issus du tableau1 ont été remplacés par les fréquences marginales

NB : la somme des f.j et fi. doivent être égales à 100%
Remarque :
Lorsque la variable est munie d'une relation d'ordre, on peut calculer des fréquences marginales cumulées.





