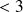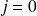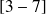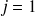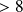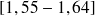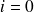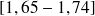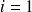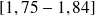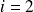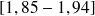Indépendance de 2 variables qualitatives
Soit deux variables qualitatives X et Y ayant respectivement I et J modalités. X est dite indépendante de Y si et seulement si les distributions conditionnelles de X pour toutes les modalités de Y sont constantes. Autrement dit les fréquences conditionnelles des modalités i (i=1, ...,I) de X ne changent pas quelles que soient les modalités j (j=1, ..., J) de Y.
Cela se traduit par la formule suivante :
(1)
Réciproquement, Y est dite indépendante de X si et seulement si les distributions conditionnelles de Y pour toutes les modalités de X sont constantes. Autrement dit les fréquences conditionnelles des modalités j (j=1, ..., J) de Y ne changent pas quelles que soient les modalités i (i=1, ..., I) de X.
Cela se traduit par la formule suivante :
(2)
Nous avons vu précédemment :
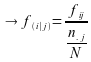
Alors
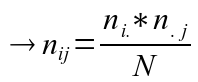
À partir de (4) nous déduisons la définition suivante :
Un tableau de contingence construit à partir de 2 variables qualitatives X et Y indépendantes présente les lignes (respectivement les colonnes) proportionnelles entre elles.
Exemple :
Considérons les données résumées dans le tableau 1. Le tableau 6 suivant présente les effectifs partiels si les variables Taille et VerreAlcool étaient indépendantes.
Tableau 6: Les effectifs partiels si les variables X et Y étaient indépendantes
X=Taille Y = VerreAlcool | Nombre de verres d'alcool consommés pendant la soirée | ||||
|---|---|---|---|---|---|
|
|
| Total | ||
Taille des individus (en m) |
| 52 | 97,6 | 38,4 | 188 |
| 96,7 | 181,7 | 71,5 | 350 | |
| 70,5 | 132,4 | 52,1 | 255 | |
| 18,8 | 35,3 | 13,9 | 68 | |
Total | 238 | 447 | 176 | 861 | |