Intervalle de confiance (IC) : échantillon --> population
Remarque : Pour la situation inverse
induction (inférence) de l'échantillon --> la population
L'objectif de l'inférence est d'obtenir une estimation de la valeur d'un paramètre (une moyenne, une proportion ou une variance) dans la population à partir de ce que l'on observe dans un échantillon. La statistique sert presqu'exclusivement à faire de l'inférence, très rarement à faire de la prédiction.
à partir d'une moyenne
et d'une variance
observées, que peut-on dire de la valeur de
?
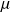l'intervalle de confiance (IC) de
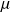sera :
et si
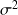est connue :
Si petit échantillon --> loi de Student :
à partir d'une moyenne (et variance) observée
l'IC de
:
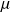la valeur de
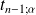se lit dans la table de Student
Remarque :
l'IC donne une plage de valeurs de
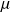compatibles avec les observations
L'intervalle de confiance d'un paramètre est défini de la manière suivante :
Si l'on répéte un tirage au sort un nombre de fois infini, 95 % des intervalles définis comme précédemment (voir diapo précédente) contiennent la vraie valeur (inconnue) du paramètre
souvent (et abusivement) formulé autrement :
L'intervalle de confiance d'un paramètre est ...
... l'intervalle de valeur qui a 95\% de chance de contenir la vraie valeur du paramètre
on fait référence à un nombre infini de répétition de l'échantillonnage mais en pratique on ne calcul qu'un seul intervalle de confiance !
en calculant IC de
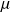, on réalise une inférence sur
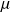
il s'agit d'une estimation par intervalle : on estime la valeur de
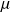par l'intervalle de valeurs qui peut raisonnablement contenir la valeur de
