Une autre formulation : le test statistique
On cherche souvent à savoir si une moyenne diffère d'une valeur attendue
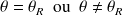
ou si les moyennes de deux groupes diffèrent :
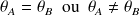
en tenant compte de l'incertitude sur
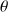 ou sur
ou sur
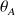 et
et
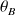
donc en tenant compte de leur intervalle de confiance
passage d'une estimation par intervalle à une comparaison de deux valeurs ponctuelles
passer d'une estimation par intervalle à une valeur précise pour savoir si cette valeur peut être acceptée ou doit être rejetée comme valeur de la population
sachant
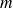 , peut-on exclure que
, peut-on exclure que
 ?
?sachant
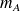 et
et
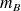 , peut-on exclure que
, peut-on exclure que
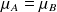 ?
?
Voyons quelques exemples...
Exemple : Exemple 1
On souhaite savoir si une pathologie pancréatique donnée
 est susceptible de provoquer une hyperglycémie à jeun.
est susceptible de provoquer une hyperglycémie à jeun.
on réalise une étude sur 55 patients atteints de la maladie
on suppose que
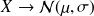
on observe les valeurs
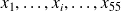
on peut estimer
 et
et
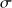 par
par
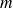 et
et
 (voir cours précédents)
(voir cours précédents)soit
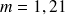 et
et
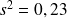
comment savoir si dans cette pathologie la glycémie moyenne
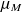 est supérieure à la valeur de référence
est supérieure à la valeur de référence
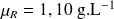 ?
?sachant
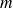 et
et
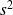 (échantillon) et que 14 sujets parmi les 55 ont une glycémie normale
(échantillon) et que 14 sujets parmi les 55 ont une glycémie normale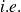 est-ce que dans cette population de malades
est-ce que dans cette population de malades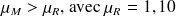 ?
?comment tenir compte de l'aléatoire dans cette comparaison ?
Exemple : Exemple 2
Soit un caractère génétique
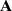 dont on ne sait pas s'il suit les lois de Mendel (dominant/récessif -
dont on ne sait pas s'il suit les lois de Mendel (dominant/récessif -
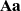
le vrai mode de transmission du caractère est inconnu
un échantillon de 200 sujets issus de croisement de
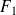
130 sujets de phénotype
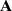 (soit
(soit
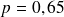 )
)la proportion observée
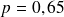 est-elle compatible avec une transmission mendélienne (soit
est-elle compatible avec une transmission mendélienne (soit
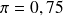 ) ?
) ?
notion d'hypothèse à tester :
tester si une hypothèse sur un paramètre est vérifiée ou pas à la vue des données
l'hypothèse sur le paramètre traduit l'hypothèse scientifique\
On souhaite souvent pouvoir affirmer (statistiquement...) qu'un paramètre (de position, de dispersion, de relation entre variables) dans une population (mais observé sur un échantillon) a une certaine valeur ou au contraire diffère d'une certaine valeur de référence.
Ceci implique de pouvoir tester la valeur observée pour savoir si elle diffère d'une valeur de référence.
Cette approche est un des modes d'acquisition de connaissances scientifiques.
Exemple :
Sur une série de
 naissances, on observe un poids moyen de 3250 g. Ce poids moyen est-il conforme à la moyenne nationale ?
naissances, on observe un poids moyen de 3250 g. Ce poids moyen est-il conforme à la moyenne nationale ?
Remarque :
Dans les exemples, il s'agit en fait d'un couple d'hypothèses et non pas d'une hypothèse unique :
cas de la maladie pancréatique :
hypothèse de référence : la glycémie à jeun moyenne chez les malades est inférieure ou égale à la valeur de référence :
 , où
, où
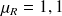
hypothèse alternative : la glycémie à jeun moyenne est supérieure à la moyenne de référence
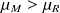
cas de la transmission mendelienne :
hypothèse de référence : la transmission est mendélienne et
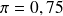
hypothèse alternative : la transmission n'est pas mendélienne et
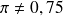
On peut déjà noter une certaine asymétrie entre les hypothèses : l'une représente ce que le chercheur espère démontrer
Sur ces deux exemples :
S'il y a une différence entre la moyenne (resp. proportion) attendue et la moyenne (resp. proportion) observée, l'écart est dû :
soit uniquement à une fluctuation d'échantillonnage
soit à une fluctuation d'échantillonnage \emph{et} à une différence causée par un facteur séparant le groupe de la population de référence
Comment distinguer ces deux cas sans se tromper ?
Ou, à défaut, en se trompant le moins souvent possible ?
Le test statistique formalise cette comparaison entre deux hypothèses en tenant compte du caractère aléatoire des données
Le test statistique permet de prendre des décisions
en situation d'incertitude (échantillons aléatoires)
acquisition de connaissances scientifiques

l'hypothèse biologique sera convertie en hypothèse statistique, avec une formulation mathématique





