Statistiques de base

"Estimer ne coûte presque rien

Estimer incorrectement coûte cher"

Vieux proverbe chinois

Dans le domaine de la santé comme dans de nombreux autres domaines, on a besoin de connaître certaines caractéristiques de la population ciblée par une étude. En règle générale, il est difficile voire impossible d'évaluer ces caractéristiques sur la population (effectif trop important, coût trop élevé, durée de réalisation trop longue). On est alors conduit à estimer ces caractéristiques à partir des observations sur un échantillon de plus petite taille issu de la population.

La qualité de l'estimation d'un paramètre tel que la moyenne, la variance ou la proportion d'un caractère et donc celle de l'information obtenue repose sur la prise en compte de plusieurs éléments.

• La représentativité de l'échantillon

  L'échantillon doit être représentatif de la population ciblée et une façon d'obtenir un échantillon représentatif est de réaliser un tirage au sort aléatoire, simple ou stratifié, parmi les N individus constituant la population (Cf. chapitre 9 – Notion de population et d'échantillon).

• L'utilisation d'un bon estimateur pour l'estimation ponctuelle du paramètre

  Nous verrons que l'estimateur d'un paramètre est une expression mathématique des mesures ou des observations de l'échantillon. Ces estimateurs doivent posséder certaines propriétés qui ne figurent pas au programme de ce cours.

• La fluctuation d'échantillonnage

  Un échantillon, même tiré au sort dans la population ciblée, n'est pas l'image exacte de la population en raison de ce que l'on appelle la fluctuation d'échantillonnage.

  Par exemple, si l'on tire au sort des échantillons dans une population contenant 20% de personnes avec des yeux bleu, on obtient des échantillons où la proportion de sujets aux yeux bleus fluctue autour de 20%. Ces fluctuations sont imprévisibles et le hasard peut conduire à des écarts (par rapport à 20%) plus ou moins importants. Cependant les grands écarts sont très peu probables et l'on pourra calculer des intervalles autour de la valeur observée dans l'échantillon tel qu'une grande proportion (ou probabilité) d'entre eux contiennent la valeur de 20%. Il s'agit des intervalles de confiance.

• L'erreur commise sur l'estimation, ou impression

  Elle est calculée à partir de l'intervalle de confiance et qui dépend en particulier de la taille de l'échantillon.

Dans ce chapitre nous allons apprendre à estimer, à l'aide des observations faites sur un échantillon, les paramètres suivants :

• - moyenne (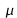) et variance 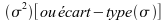dans le cas d'une variable quantitative

• proportion (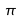) dans le cas d'une variable qualitative.

Nous envisagerons l'estimation ponctuelle, l'estimation par intervalle et l'imprécision de l'estimation pour chacun des paramètres.