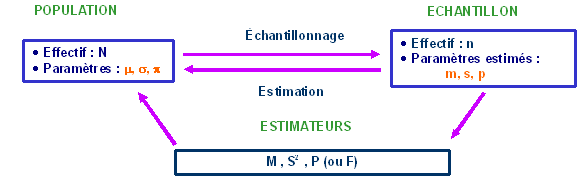
Procédure générale d'estimation d'un paramètre
Soit une variable X (quantitative ou qualitative) et sa loi de distribution (ou de probabilité) pour la population ciblée telles que la loi de Gauss ou loi normale N(
,
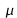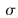), la loi binomiale B(n,p).On dispose des n observations de la variable X sur un échantillon (noté n-échantillon) issu de la population : x1, x2,.....xi, ......xn
NB : x1, x2,.....xi, ......xn sont les réalisations des n variables X1, X2,....Xi, ....Xn qui suivent la même loi de distribution que la variable X.
On cherche à obtenir la valeur d'un paramètre θ (
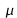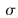, ou
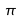) de la loi de distribution de X.La procédure d'estimation a pour objectif de trouver la meilleure valeur approchée du paramètre θ à partir des n observations de l'échantillon.
Cela nécessite de disposer du meilleur estimateur de ce paramètre.
Un estimateur est une fonction mathématique reliant le n variables Xi, c'est donc une variable aléatoire.
Exemple :
L'expression de l'estimation de la moyenne est :
A partir des n observations xi de l'échantillon on obtiendra, en utilisant l'estimateur, une valeur du paramètre θ qui constitue l'estimation ponctuelle de ce paramètre.
L'estimation ponctuelle de la moyenne () sera égale à :
L'estimation ponctuelle du paramètre θ étant influencée par les fluctuations d'échantillonnage, il faudra lui associée une estimation par intervalle : on calculera un intervalle de confiance (IC) qui nécessite de connaître la loi de distribution du paramètre estimé.
L'intervalle de confiance permettra d'évaluer l'impression de l'estimation du paramètre.
La figure ci-dessous représente les étapes et les notations associées à la procédure d'estimation.
