Contexte
Considérons les 4 tables de données suivantes représentant les mesures de 2 variables au cours de 4 études différentes :
Tableau 10 : Etude N°1
X | Y |
|---|---|
22,59 | 1,16 |
22,69 | 0,56 |
22,79 | 2,05 |
21,90 | 0,65 |
22,14 | 0,95 |
23,91 | 2,07 |
24,39 | 3,39 |
22,99 | 0,08 |
24,80 | 3,85 |
23,54 | 2,01 |
22,89 | 1,57 |
23,75 | 2,34 |
Tableau 10 : Etude N°2
X | Y |
|---|---|
30,10 | 1,72 |
31,08 | 0,52 |
28,74 | 1,72 |
32,79 | 0,43 |
30,46 | 2,38 |
32,53 | 0,02 |
30,55 | 0,91 |
32,20 | 0,98 |
27,65 | 3,76 |
32,59 | 0,01 |
28,62 | 2,26 |
30,55 | 0,99 |
Tableau 10 : Etude N°3
X | Y |
|---|---|
22,66 | -0,49 |
24,07 | 0,01 |
23,68 | 1,16 |
22,89 | 3,58 |
20,82 | 1,49 |
23,34 | 0,97 |
23,80 | 1,59 |
23,46 | -3,46 |
24,69 | 1,18 |
24,39 | -2,90 |
20,84 | 0,47 |
25,31 | 1,26 |
Tableau 10 : Etude N°4
X | Y |
|---|---|
30,65 | -0,10 |
28,65 | -0,06 |
31,10 | -0,05 |
29,29 | -0,13 |
29,93 | -0,15 |
31,22 | -0,03 |
33,68 | 0,12 |
30,61 | -0,11 |
30,85 | -0,08 |
31,68 | 0,04 |
29,07 | -0,11 |
34,70 | -0,02 |
Il s'agit ici de variables aléatoires continues et la question est de savoir si les 2 variables X et Y sont liées entre elles dans les différentes études.
Exemple :
Existe-t-il une relation entre le poids (PDS) d'un individu et son indice de masse corporelle (IMC) ?
La réponse ici est oui car nous connaissons la relation qui lie le poids à l'IMC :
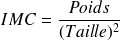
Existe-t-il une relation entre une mesure du tour de tête et le quotient intellectuel (QI) ?
Quelle est la relation entre le dosage de la ferritine et celui de CRP au cours d'un syndrome inflammatoire ? (ferritine et CRP étant 2 marqueurs de l'inflammation).
Pour préciser nos idées, observons la représentation graphique des données des études N°1 et N°2.


Ces graphiques représentent ce que l'on appelle les « nuage de points ». Chaque point du nuage représente un couple de valeurs et chaque valeur appartenant à l'une ou l'autre des 2 variables.
Sans aucunes autres informations sur les données nous pouvons d'ores et déjà noter les éléments suivants :
Les nuages N°1 et 2 décrivent une forme globalement linéaire. C'est-à-dire que nous pouvons tracer une droite qui suivrait la direction d'une majorité des points. Cette est représentée pour la figure N°2 en noire.
Sur la figure 1, lorsque X augmente, Y augmente également (Flèche rouge et verte) et,
Sur la figure 2, lorsque X augmente, Y a tendance à diminuer
Regardons ce qui se passe pour les données des 2 autres études :


Sur la figure 3, le nuage de point ne présente pas de forme apparente comme c'était le cas pour les nuages 1 et 2. De plus on ne peut pas décrire l'évolution de X par rapport à Y.
Sur la figure 4, on arrive à identifier une forme sinusoïde des points.
Rappel : Récapitualtif
Sur les nuages N°1,2 et 4, nous pouvons dire que la variable X est liée à la variable Y :
On peut identifier une relation linéaire entre X et Y dans laquelle ces dernières évoluent dans la même direction (Nuage N°1)
On peut identifier une relation linéaire entre X et Y dans laquelle ces dernières évoluent dans les directions opposées (Nuage N°2)
Dans le Nuage N°4 la relation linéaire n'est pas aussi évidente que dans les cas précédents, néanmoins les variables X et Y semblent être liée.
Sur le nuage N°3, nous pouvons dire que les variables X et Y évoluent chacun pour leur compte. C'est-à-dire la direction des valeurs de X n'influence pas celles des valeurs de Y.
Notion d'indépendances de 2 variables quantitatives
Attention :
Dans ce cours, la relation entre 2 variables quantitatives est définie dans le sens linéaire du terme. C'est-à-dire que 2 variables sont dites liées entre elles lorsque qu'il existe une droite permettant de décrire d'une part la direction (ou le sens) de l'évolution des valeurs et d'autre part la force de cette liaison.
Nous dirons que 2 variables quantitatives sont indépendantes l'une de l'autres lorsque l'évolution des valeurs de l'une (quelle que soit la direction) n'influence pas celle des valeurs de l'autre. Autrement dit, il n'a aucune relation linéaire évidente entre les 2 variables (voir la figure 3).
Deux indicateurs statistiques permettent de caractériser cette notion d'indépendance :
La covariance et la corrélation.





