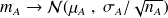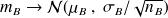Grands échantillons
Comparaison de deux moyennes observées
(1) cas des grands échantillons :
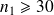 et
et
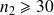
On admet qu'un échantillon est grand quand son effectif
 est supérieur ou égal à 30 ; ceci est partiellement arbitraire.
est supérieur ou égal à 30 ; ceci est partiellement arbitraire.
Dans ce cas (
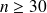 ), alors la moyenne
), alors la moyenne
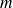 suit une loi de Gauss. Cela signifie que si l'on pouvait faire un nombre infini d'échantillons dans la même population, alors l'histogramme des moyennes de cette infinité d'échantillons aurait la forme d'une loi normale.
suit une loi de Gauss. Cela signifie que si l'on pouvait faire un nombre infini d'échantillons dans la même population, alors l'histogramme des moyennes de cette infinité d'échantillons aurait la forme d'une loi normale.
Si on connait la distribution théorique des données dans la population dont on extrait les échantillons, on peut préciser les caractéristiques de la loi de Gauss qui caractérise la moyenne des échantillons : sa moyenne sera
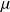 et l'écart-type de la moyenne (= erreur-standard)
et l'écart-type de la moyenne (= erreur-standard)
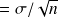 .
.
Pour la différence de deux moyennes, on a le même résultat dans chaque groupe, soit :
Pour la différence de ces deux moyennes, un résultat similaire s'applique : si il n'y a pas de différence entre les deux groupes, et si on connait la distribution des valeurs dans la population (constituée des deux populations d'intérêt qui sont en fait identiques sous l'hypothèse d'absence de différence), alors la loi de la différence des moyennes suit une loi de Gauss dont les paramètres sont :

Ceci est vrai seulement si les deux échantillons sont indépendants.
La plupart du temps, les
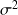 ne sont pas connues
ne sont pas connues
Comme
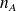 et
et
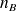 sont grands, on peut remplacer
sont grands, on peut remplacer
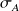 et
et
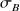 par leurs valeurs observées
par leurs valeurs observées
 et
et
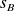 (bonne approximation)
(bonne approximation)
alors, sous l'hypothèse d'égalité des variances :
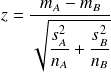
Il y a ici deux approximations de nature différente :
la distribution de
 par une loi normale
par une loi normalecelle de la valeur de
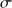 par
par

Pour un test bilatéral :
si
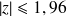 on accepte
on accepte
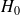 : absence de différence
: absence de différencesi
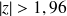 on conclut
on conclut
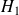 : différence des moyennes
: différence des moyennes
Et pour un test unitaléral :
pour
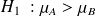 alors rejet de
alors rejet de
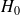 si
si
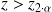
pour
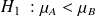 alors rejet de
alors rejet de
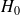 si
si
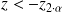
En pratique : on calcule la valeur de
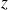 (voir formule plus haut et exemple plus loin) et on la compare à la valeur de référence de la loi normale pour le
(voir formule plus haut et exemple plus loin) et on la compare à la valeur de référence de la loi normale pour le
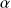 consentie. En général
consentie. En général
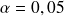 et
et
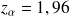 .
.
Application
Exemple : Somnifères
Deux traitements
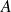 et
et
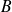 (
(
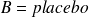 ), comparés sur la durée de sommeil
), comparés sur la durée de sommeilon observe
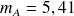 ,
,
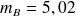 ,
,
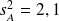 et
et
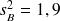 ,
,
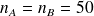
formulation unilatérale
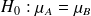 et
et
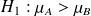
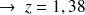 (
(
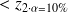 = 1,645), donc différence non significative
= 1,645), donc différence non significativedonc
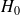 , l'absence de différence est ici retenue et on conclut que l'on ne met pas en évidence de différence entre les deux traitements (remarque : on n'affirme pas l'égalité des moyennes)
, l'absence de différence est ici retenue et on conclut que l'on ne met pas en évidence de différence entre les deux traitements (remarque : on n'affirme pas l'égalité des moyennes)0,39 h = 23 mn : gain non négligeable mais insuffisant pour montrer la supériorité de A sur un placebo avec les effectifs considérés