Séries appariées
Comparaison de moyenes sur séries appariées
Jusqu'ici deux groupes indépendants de valeurs
mais parfois les mesures ne sont pas indépendantes
notion de comparaison non-indépendantes entre deux groupes
Exemple :
comparaison de valeurs mesurées avant et après l'application d'un traitement chez les mêmes sujets (habitant d'une ville dont on mesure le poids avant et après la mise en place d'un programme de promotion de l'activité physique)
témoins appariés à des cas, avec appariement par âge, taille, critères biologiques, etc : les sujets sont différents mais on les rends « comparables » par l'appariement
côté droit / côté gauche : application d'une crème A solaire sur la main droite et d'une crème solaire B sur la main gauche
Principe de la solution
pour le sujet
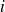, calcul de la différence entre les deux valeurs
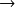une série unique de
valeurssi les deux moyennes ne diffèrent pas, la moyennes des différences sera nulle
-
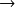comparer la moyenne de cette série à 0.
= un test contre une moyenne de référence
Donc, pour chaque sujet, on calcule
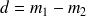
le test statistique :
(
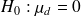) et
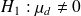
deux tests selon les effectifs :
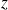si
grand ou
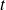si
petit
Si
est grand, alors on utilise un test
:
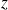Si
est petit (
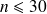, alors on utilise un test
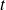, qui a en fait la même formule que le test
:
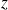Remarque :
La formule est la même ! La différence tient dans le fait d'utiliser la table de la loi normale ou la table de la loi de Student (à $n-1$ ddl) pour chercher la valeur seuil lors de la réalisation du test.
Exemple : Comparaison de glycémie à jeun sans et avec un traitement chez les mêmes sujets
l'absence d'effet du traitement, les écarts de mesures seront nuls
en formulation bilatérale
:
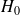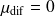et
:
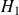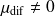
soit
,
,
*
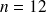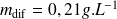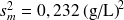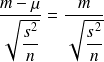car
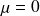et
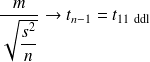
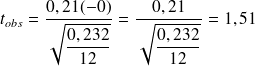
donc
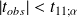
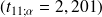
d'où le non rejet de
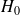: le médicament ne semble pas modifier la valeur de la glycémie à jeun
