Petits échantillons
Comparaison de deux moyennes observées
(2) cas des petits échantillons : un échantillon (ici avec deux groupes) est considéré comme « petit » si
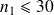et/ou
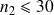
Fluctuations d'échantillonnage sous
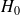(i.e. si
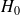est vraie) :
dans ce cas, l'approximation par la loi de Gauss n'est plus possible
en raison de l'estimation des variances
Il faut alors utiliser une autre loi de probabilité : la loi de Student. Cette loi est similaire à la loi de Gauss. Elle va de moins l'infini à plus l'infini, a une moyenne et une variance. La principale différence avec la loi de Gauss est la présence d'un paramètre supplémentaire : les degrés de liberté, qui dépendent des effectifs des échantillons.
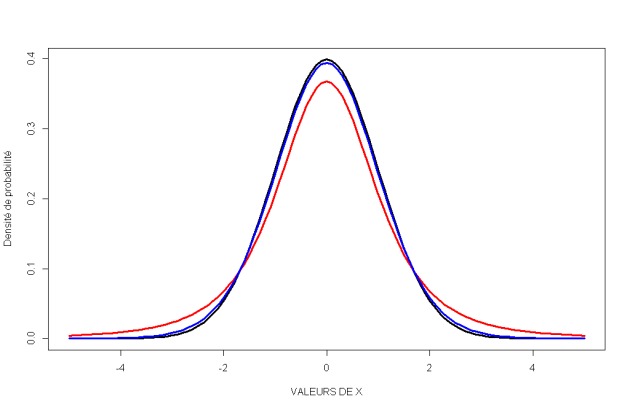
La loi de Student
La loi de Gauss est en noir. La loi de Student (en vert et en rouge) a une forme qui dépend des degrés de liberté. Plus les degrés de libertés sont élevés, plus la loi de Student se rapproche de la loi de Gauss (en rouge ddl= 3 et en vert ddl = 20). Pour
supérieur à 30, la différence entre les deux lois est négligeable.
Réalisation du test
si la distribution de la variable aléatoire est gaussienne dans chacune des populations et si
(homogénéité des variances), alors :
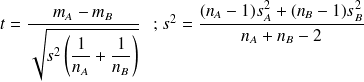
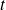à
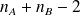ddl} ;
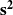: moyenne pondérée des variances
La valeur de
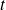suit une loi de Student à
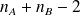ddl.
Donc, pour un test bilatéral :
on rejette
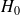si
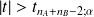
Et pour un test unilatéral :
pour
alors rejet de
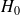si
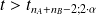
pour
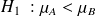alors rejet de
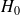si
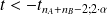
Si la V.A. d'intérêt suit une loi de Gauss et que les variances sont égales.
Le test
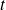est en fait valable même pour de grands effectifs, car il se rapproche d'un
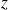quand les effectifs augmentent (voir graphique plus haut) .Dans le cas des grands échantillons, il y a donc deux tests utilisables, qui donnent des résultats très proches.
Lorsque les effectifs sont inégaux, il est particulièrement important que l'homoscédasticité des variances soit respectée
Lecture de la table de la loi de Student
Pour lire la table de la loi de Student et trouver la valeur seuil, procéder de la manière suivante :
prendre la table de la loi de Student
définir le nombre de degré de liberté pour le problème considéré : d.d.l. =
dans la table choisir la ligne correspondant au nombre de d.d.l.
allez jusqu'à la colonne correspond au risque $\alpha$ choisi : si
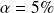et que le test est en bilatéral, prendre la colonne « 100-5/2 = 97,5% » c.-à-d. 0,975 ; si le test est unilatéral, prendre la colonne « 100-5% = 95% » c.-à-d. 0,95notez la valeur seuil à l'intersection de la ligne ddl et de la colonne en fonction de
comparer la valeur calculée dans le test et la valeur seuil trouvée dans la table.
Application
Exemple : Tension artérielle
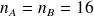
on observe
,
,
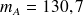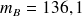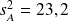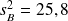
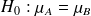et
et
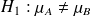
on calcule :
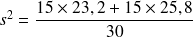
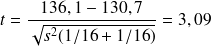
donc
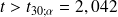
formulation bilatérale car effet du toxique inconnu a priori
on utiliserait une formulation unilatérale par ex. pour un traitement dont on connait l'action pharmacologique
Synthèse sur les conditions d'application
Différents cas possibles :
soit une variable aléatoire
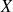(poids, taille, revenu etc)si les effectifs sont grands (
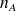et
)
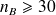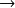test
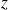quelle que soit la loi de
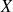
si les effectifs sont petits (
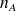et
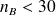) ou si l'un des effectifs est petit (
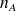ou
)
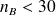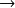test
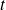mais alors :-
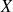doit être gaussien
les variances ne doivent pas être différentes
on utilise la moyenne pondérée des variances
