Présentation intuitive
(1) Soit une urne composée de deux compartiments remplis d'un très grand nombre de boules bleues (premier compartiment) et de boules rouges (second compartiment)
les boules ont des tailles variables mais on sait que leur taille moyenne des bleues est identique à la taille moyenne des rouges ; la dispersion des tailles est également identiques dans les deux compartiments (= paramètres de la population des boules rouges et des boules bleues)
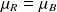et
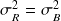
on procède à l'extraction d'un échantillon de
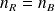boules dans chaque compartimentcalcul de
,
,
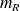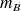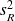et
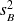(valeurs observées) et écart
remise dans l'urne
et on répéte l'opération un très grand nombre de fois.
dans chaque échantillon, on observera une taille moyenne
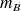pour les boules bleues et une taille moyenne
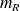pour les boules rougesde même, on observera deux variances
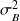et
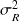
l'écart entre les deux moyennes variera autour d'une différence nulle
on obtient alors une distribution des moyennes, distribution standardisée, sous l'hypothèse d'absence de différence
En général, l'écart entre les moyennes sera "petit"
(2) Soit une seconde urne, avec une composition différente :
les boules ont des tailles variables,
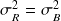et
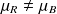
extraction d'un échantillon de
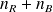boules,
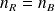
calcul de
,
,
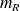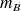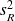et
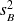(valeurs observées) et écart
remise dans l'urne
et on répète l'opération un très grand nombre de fois
distribution des moyennes standardisées sous l'hypothèse de l' existence d'une différence
En général, l'écart entre les moyennes sera "grand"La proportion de cas où l'écart est grand dépend de l'ampleur de l'écart des moyennes
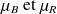, des variances
et des
Présentation intuitive
Remarque :
Mais dans la pratique, on ignore la composition de l'urne
1 :
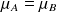ou 2 :
?
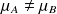et on ne travaille que sur un échantillon, unique.
Détour par la pratique :
que signifie on ignore la composition de l'urne ? Lorsque l'on souhaite savoir si les sujets obèses sont plus fréquement tabagiques que les sujets non obèses, on ne peut qu'observer un échantillon de sujets, composé de sujets obèses et de sujets non obèses, et comparer les proportions de sujets tabagiques. La proportion de sujets tabagiques dans la population de sujets obèses et dans la population de sujets non obèse ne peut pas être connue exactement car il faudrait pouvoir interroger la totalité de chacune de ces population, ce qui n'est pas faisable en pratique. D'où l'intérêt de la statistique pour conclure sur une population inaccessible à partir d'un échantillon accessible, avec un certain risque d'erreur consenti dans la conclusion.
Retour à la théorie :
Donc :
on tire un échantillon de boules sans savoir de quelle urne il est extrait, on calcule
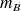et
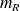et l'écart
comment savoir si l'échantillon provient de l'urne avec une différence ou s'il vient de l'urne sans différence ?
le test statistique ou test d'hypothèse ou encore test d'hypothèse nulle propose une solution à cette question
