Le test d'hypothèse : première synthèse
On définit deux hypothèses :
1 - celle que l'on espère pouvoir montrer comme étant fausse : hypothèse nulle
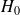
2 -celle que l'on espère vérifier comme étant vraie : hypothèse alternative
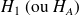
Exemple :
on veut montrer qu'un traitement B est plus efficace qu'un traitement de référence A :
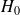on espère invalider le fait que B ne soit pas supérieur à A
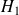on espère vérifier que B est supérieur à A
Ce que l'on vient de dire revient à comparer deux hypothèses :
soit l'échantillon vient de la population
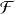
soit l'échantillon ne vient pas de la population
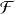mais de la population
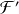
Soit, en terme de paramètres :
soit
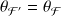
soit
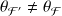
Ces deux hypothèses constituent respectivement l'hypothèse nulle
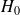et l'hypothèse alternative
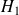ou
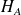et
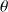correspond soit à une proportion, soit à une moyenne selon le contexte.
D'autres types de paramètres peuvent être testés (corrélation,...)
Il y a donc deux hypothèses que l'on souhaite pouvoir départager.
le test permet de décider parmi deux hypothèses complémentaires portant sur un paramètre statistique laquelle est "vraie",
retenue comme vraiele test permet des conclusions tenant compte de l'incertitude de la décision
mais en raison de l'aléa, la décision n'est jamais certaine
En prenant une décision en situation aléatoire, 4 situations peuvent survenir :
deux manières d'avoir raison
retenir l'hypothèse d'égalité quand elle existe
affirmer l'hypothèse d'une différence quand elle existe
deux manières d'avoir tort
retenir l'égalité quand il y a une différence
affirmer la différence quand il y a égalité
En réalisant un test statistique, il y a donc deux types d'erreur possible ayant chacune un certain risque d'être présente
Les types d'erreur
l'erreur de première espèce
encore appelé risque α
risque d'affirmer une différence quand elle n'existe pas
risque de rejeter
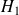quand elle est vraie
l'erreur de deuxième espèce
encore appelé risque β
risque de conclure à l'absence de différence alors qu'elle existe
risque de ne pas accepter
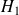quand elle est vraie
