L'hypothèse que l'on veut vérifier
Sous l'hypothèse d'un écart à la loi de Mendel, spécifier ce que l'on s'attend à trouver :
par ex.
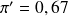au lieu de
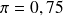.on cherche à mettre en évidence que l'écart entre les proportions est au moins de 8% (
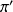inf à 0,67 ou sup à 0,83)
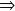calculer la probabilité de tomber dans la zone de rejet (
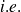moins de 69 % de
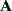) si
.
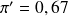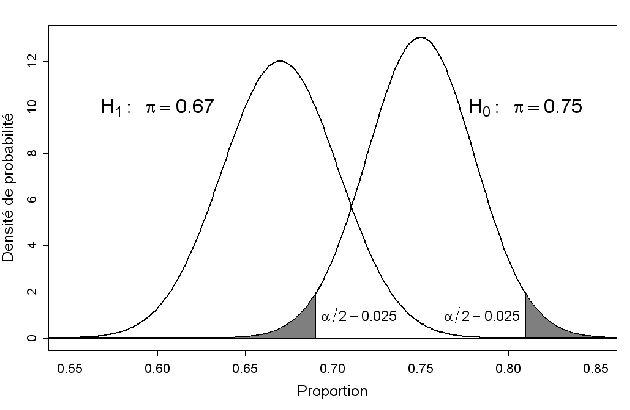
Le graphique suivant montre deux courbes. La courbe de droite est la loi de Gauss attendue sous l'hypothèse où la proportion est de 75%. En grisé se trouve les deux extrémités de la courbe telles que dans un échantillon aléatoire on ait une probabilité de 2,5% d'observer une valeur haute ou basse de la proportion.
La courbe de gauche représente la courbe attendue sous l'hypothèse où la proportion est de 67\%.
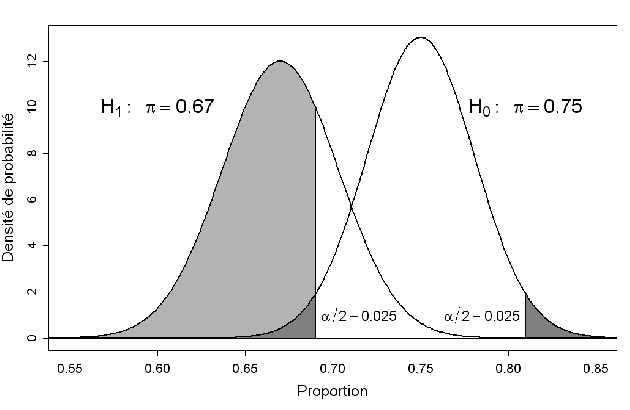
la probabilité d'être dans la zone de rejet (moins de 69% ou plus de 81% de
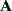) sous l'hypothèse
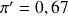vaut :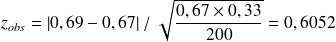
et
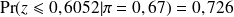
soit
avec les données dont on dispose, on a donc une probabilité de 0,726 d'être dans la zone de rejet si l'hypothèse
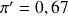est vraie : puissance du testla probabilité d'être au delà de 81\% est
inutile de la calculer
La même question peut se poser pour une moyenne : pour un échantillon
ayant une moyenne observée
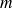, peut-on dire qu'il est extrait de la population
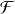ou au contraire vient-il d'une autre population
?En terme de paramètre, l'échantillon a-t-il une valeur de paramètre compatible avec la valeur du paramètre dans la population de référence ?
