Notion de zone de rejet
Dans un test statistique, on définit (arbitrairement) une zone de rejet :
Définition : Définition de la zone de rejet
ensemble des valeurs de la statistique de test (la valeur de
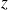, ou de
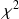, vue plus loin dans le cours) pour lesquelles on rejettera l'hypothèse de départ d'absence de différence
la zone est définie indirectement par la probabilité d'observer les données obtenues au cours de l'expérience sous l'hypothèse d'absence de différence
si cette probabilité est petite, on admet que les données observées ne sont pas compatibles avec l'hypothèse de départ et donc que cette hypothèse d'absence de différence est fausse
le plus souvent, zone de rejet = ensemble des valeurs telles que
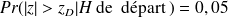
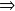probabilité "petite".donc, en pratique, on choisit une probabilité considérée comme "petite"et on trouve l'ensemble
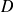qui remplit la condition ci-dessus.
Avec les données de l'exemple 2 :
à partir d'un échantillon aléatoire où 130/200 sujets ont le phénotype $A$, peut-on admettre que l'échantillon vient bien de la population de référence ?
vérification : est-on dans la zone de rejet ?
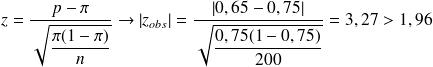
Donc :
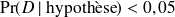
Où
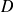: 130/200
on rejette alors l'hypothèse de départ qui dit que
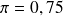car le nombre de sujets de type
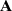est trop faible pour être compatible avec cette hypothèse
Donc :
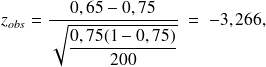
la zone de rejet
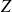peut être exprimée de trois façons différentes :
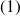
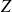: [138 sujets ou moins] ou [162 sujets ou plus]/200
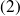
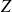: proportion $\leqslant69\%$ ou $\geqslant 81\%
:
:
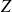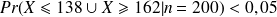événement "rare"
Si [138 sujets ou moins] ou [162 sujets ou plus]/200 alors :
rejet de l'hypothèse de départ
car :
et probabilité de cet évènement est faible (
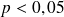) si
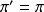
puisque
Pr([138 sujets ou moins]/200} ou [162 sujets ou plus]/200|
=0,75) = Pr(|z| > 1,96|
=0,75)} = 0,05
Remarque : Récapitulation :
il y a un couple d'hypothèses
l'hypothèse de départ est rejetée (ou non) au profit de l'autre hypothèse
l'autre hypothèse représente ce que, en général, on cherche à démontrer
ici : on cherche à montrer que le caractère étudié ne suit pas une loi de Mendel
on peut souhaiter mettre en évidence une différence ayant un intérêt clinique, par exemple par rapport à une valeur de référence
-
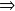se donner les moyens de trouver la différence recherchée
