Définition d'un intervalle de confiance
L'estimation ponctuelle d'un paramètre θ est influencée par les fluctuations d'échantillonnage. Il est donc nécessaire de définir une fourchette de valeurs de θ compatibles avec les observations qui constitue l'estimation par intervalle.
Le calcul des bornes (θinf, θsup) de la fourchette de valeurs, appelé intervalle de confiance (IC), repose sur la loi de distribution du paramètre θ à estimer (moyenne
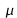, proportion 
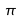, variance 
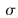²). On fixe une probabilité, notée α et correspondant au seuil ou risque d'erreur, d'avoir un écart δ entre la valeur estimée (ou observée) et la valeur vraie de θ. Pour la moyenne on aura :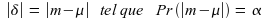
L'intervalle est symétrique en probabilité autour de la valeur estimée du paramètre.
L'IC peut être défini de la manière suivante :
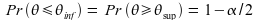
On l'exprime sous la forme :
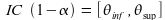
Si le risque d'erreur α est égal à 5% , on aura un IC à 95% noté IC(95).
L'interprétation de l'IC est la suivante : si l'on constitue un grand nombre d'échantillons (théoriquement un nombre infini) de même taille (n) par tirage au sort, on obtiendra autant de valeurs estimées du paramètre et d'intervalles de confiance associés. Pour un risque d'erreur α de 5%, 95% des intervalles de confiance contiennent la vraie valeur (inconnue) du paramètre.
La figure ci-dessous illustre cette interprétation (pour une moyenne
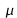) et permet de comprendre la différence entre intervalle de confiance et intervalle de pari (notion qui sera précisée dans le chapitre 11 – Notion de test d'hypothèse).
