Intervalle de confiance d'une proportion
Distribution d'échantillonnage d'une proportion
La distribution d'échantillonnage d'une proportion
est une loi binomiale
pour un échantillon de taille
. La valeur de
est généralement estimée à partir des données de l'échantillon.
Dans certaines conditions on peut faire une approximation de la loi binomiale par la loi normale. En effet, on peut montrer que si
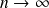
si l'on considère le nombre de succès
ou
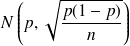si l'on considère la proportion de succès
En pratique on pourra effectuer cette approximation si
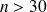et
voisin de 0,5 (on considère en général
) que l'on exprime sous la forme:
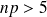et
.
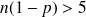Remarque :
Dans certains ouvrages les conditions sont :
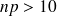et
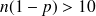
Expression de l'intervalle de confiance d'une proportion
L'intervalle de confiance peut toujours être calculé en utilisant la loi binomiale, ce qui peut s'avérer compliquer quand on ne dispose pas de logiciel ou de tables appropriés.
Le calcul est simplifié si les conditions d'approximation par une loi normale sont vérifiées.
Nous présenterons uniquement cette situation.
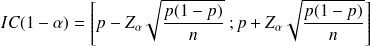
Pour
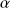= 5 %
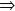
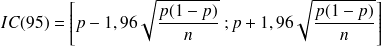
Exemples
Exemple : Exemple 5
En reprenant les données de l'exemple 2 sur l'estimation du pourcentage
d'enfants obèses ou en surcharge pondérale chez les enfants de 10 à 16 ans sur un échantillon représentatif, calculer l'intervalle de confiance à 95 % de
.On rappelle les données :
= 300,
= 0,15.Pour calculer l'intervalle de confiance à 95 % on peut utiliser la loi normale car les conditions d'approximation de la loi binomiale sont vérifiées.
est grand,
(
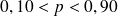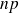= 300 x 0,15 = 45 et
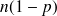= 300 x 0,85 = 255 > 30).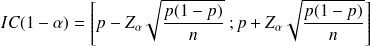
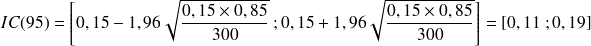
L'intervalle de confiance à 95 % est compris entre 11 % et 19 %.
Exemple : Exemple 6
Plaçons-nous dans la situation où la proportion observée d'un événement A sur deux échantillons de 20 sujets, E1 et E2, issus de deux populations très différentes est respectivement égale à 15 % et 40 %.
Pour calculer l'intervalle de confiance à 95 % on ne peut pas utiliser la loi normale pour l'échantillon E1 car les conditions de l'approximation ne sont pas vérifiés (
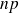= 20x0,15=3). Pour l'échantillon E2 bien que
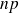et
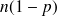soient > 5 la taille de l'échantillon est
< 30, il serait donc préférable d'utiliser la loi binomiale.
Pour E1
On obtient le résultat suivant avec la loi
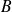(20, 0,15):
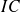(95) : [0,03 ; 0,38]On constate que l'intervalle n'est pas symétrique autour de la valeur observée 0,15.
Si on avait utilisé la loi normale on aurait obtenu le résultat suivant :
Les valeurs des bornes de l'
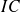sont très éloignées des valeurs exactes. De plus la valeur de la borne inférieure est négative, ce qui est impossible !!.
Cet exemple illustre bien la nécessité de respecter les conditions d'approximation de la loi binomiale par la loi normale.
Pour E2
On obtient le résultat suivant avec la loi
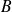(20, 0,40):
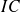(95) : [0,19 ; 0,64]On constate que l'intervalle n'est pas symétrique autour de la valeur observée 0,40.
Si on avait utilisé la loi normale on aurait obtenu le résultat suivant :
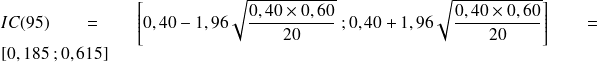
Dans ce cas les valeurs des bornes de l'
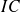sont assez proches de celles obtenues en utilisant la loi binomiale, en particulier celle de la borne inférieure.
Plus la taille de l'échantillon sera grande et la valeur de p voisine de 0,5, meilleure sera l'approximation par la loi normale.
