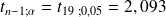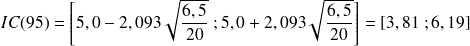Intervalle de confiance d'une moyenne
Distribution d'échantillonnage d'une moyenne
Soit une variable
qui suit une loi normale
(
,
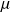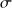). L'estimateur
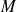de la moyenne est aussi une variable aléatoire (que l'on notera
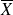de moyenne
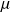et de variance
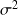/n (pour un échantillon de taille n) qui suit une loi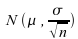 
En effet, sachant que le
variables
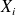suivent la même loi normale que
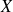, on peut en déduire :
Donc
Si la variable
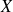est normale (ou gaussienne) et
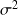connue (situation rare), la distribution de la moyenne est une loi de Gauss
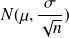, quel que soit la taille n de l'échantillon.
Si la variable
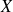est normale et
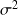inconnue (estimée par
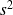), ce qui est la situation la plus fréquente, la distribution de la moyenne dépend de la taille de l'échantillon :
Si on a un grand échantillon (n
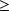30) : la moyenne suit la loi
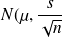
Si on a un petit échantillon (n < 30) : la moyenne suit une loi de Student à n-1 ddl
Si la variable X n'est pas normale mais si l'échantillon est de grande taille (n > 30), la distribution de la moyenne est approximativement décrite par la loi
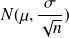si la variance
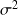est connue
et
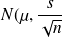si la variance
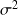est inconnue (estimée par
)
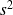Expression de l'intervalle de confiance d'une moyenne
On dispose des valeurs estimées de la moyenne et de la variance (
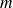et
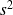) sur un n-échantillon aléatoire. Le calcul de l'intervalle de confiance de
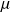(correspondant à l'intervalle de fluctuation) au risque d'erreur
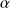dépend de la loi de distribution de la moyenne donc de la taille de l'échantillon.
• Si on a un grand échantillon (n
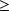30)
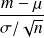
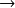
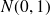On aura donc :
soit 
A partir de la valeur de la moyenne m et de la variance
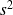, estimées sur l'échantillon, on peut calculer l'intervalle de confiance de
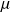au risque d'erreur
.
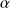L'intervalle de confiance
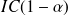de
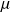sera :
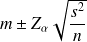
Si
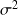est connue on aura :
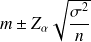
Il est exprimé de la manière suivante :
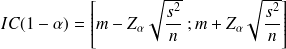
Pour
= 5 %
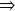
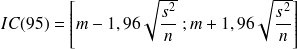
• Si on a un petit échantillon (n < 30)
A partir de la valeur de la moyenne
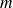et de la variance
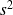, estimées sur l'échantillon, on peut calculer l'intervalle de confiance de
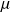au risque d'erreur
.
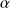L'intervalle de confiance
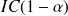de
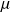sera
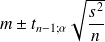
Il est exprimé de la manière suivante :
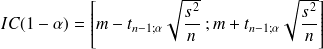
Pour
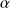= 5 % et
= 25
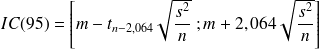
Exemples
Exemple : Exemple 3
En reprenant les données de l'exemple 1 concernant le dosage d'un paramètre biologique
sur un échantillon de sujets issus d'une population présentant une allergie particulière, calculer l'intervalle de confiance de la moyenne du paramètre
pour la population de sujets présentant cette allergie.On rappelle les données :
= 120,
= 35,0 IU et
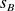= 15,08 UI.On ne connaît pas la loi de distribution de la variable
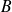mais l'échantillon étant de grande taille (
= 120 > 30), l'intervalle de confiance de la moyenne (
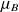) au risque d'erreur
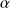= 5 %, noté intervalle de confiance à 95 %, est égal à :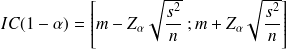
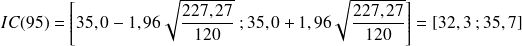
Exemple : Exemple 4
On a effectué le dosage du cholestérol sanguin chez 20 sujets appartenant à la population générale et sélectionnés par tirage au sort. La moyenne de la cholestérolémie des 20 sujets est égale à 5,0 mmoles/l, et la variance des 20 mesures est égale à 6,5 (mmoles/l)2. Sachant que la cholestérolémie
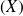dans la population générale suit une loi normale, quel est l'intervalle de confiance de la moyenne
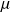de X ?Sachant que la cholestérolémie
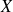suit une loi normale dans la population générale et que l'échantillon, d'effectif < 30, est représentatif de la population car constitué par tirage au sort, l'intervalle de confiance à 95% de la moyenne (
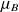) exprimé en mmoles/l est égal à :
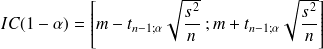avec
