Imprécision de l'estimation d'une moyenne et d'une proportion
Imprécision de l'estimation d'une moyenne
Dans le cas d'un grand échantillon, l'IC d'une moyenne est égale à :
Dans le cas d'un petit échantillon, on remplace
par
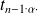
L'imprécision absolue est égale à : 
L'imprécision relative est égale à : 
Exemple : Exemple 7
Calcul de l'imprécision d'une moyenne en reprenant les données des exemples 3 et 4.
Exemple 3 : Dosage d'un paramètre biologique B sur un échantillon de sujets issus d'une population présentant une allergie particulière.
Données :
= 120,
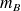= 35,0 IU,
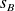= 15,08 UI et
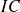(95) = [32,3 ; 35,7]
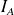= (35,7 - 32,3) / 2 = 1,7UI
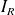= 1,7 / 35,0 = 0,0485 soit 4,85% arrondi à 5%Exemple 4 : Dosage du cholestérol sanguin sur un échantillon appartenant à la population générale.
Données :
= 20,
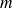= 5,0 mmoles/l IU,
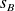= 2,55 et
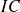(95) = [3,81 ; 6,19]
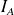= (6,19 - 3,81) / 2 = 1,19UI arrondi à 1,2 UI
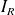= 1,19 / 5,0 = 0,238 soit 23,8% arrondi à 24%
Imprécision de l'estimation d'une proportion
Dans le cas d'un grand échantillon, l'IC d'une proportion est égale à :
L'imprécision absolue est égale à : 
L'imprécision relative est égale à : 
Dans le cas d'un petit échantillon, on utilise l'IC calculé à l'aide de la loi binomiale.
Exemple : Exemple 8
Calcul de l'imprécision d'une proportion en reprenant les données des exemples 5 et 6.
Exemple 5 : Estimation de la proportion
d'enfants obèses ou en surcharge pondérale chez les enfants de 10 à 16 ansDonnées :
= 300,
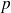= 0,15 et
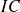(95) = [0,11 ; 0,19]
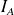= (0,19 - 0,11) / 2 = 0,04 soit 4%
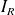= 0,04 / 0,15 = 0,267 soit 26,7% arrondi à 27%On peut noter que l'imprécision relative est importante bien que l'échantillon soit de grande taille.
Exemple 6 : Estimation de la proportion réalisée sur l'échantillon E2 à l'aide de la loi binomiale.
Données :
= 20,
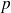= 0,40 et
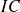(95) = [0,19 ; 0,64]
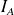= (0,64 - 0,19) / 2 = 0,225 soit 22,5%
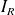= 0,225 / 0,4 = 0,56 soit 56%L'imprécision absolue et l'imprécision relative sont très importantes dans le cas d'un petit échantillon.
