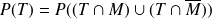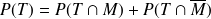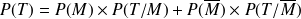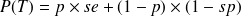Le théorème de Bayes
Le théorème de Bayes permet, de déterminer une probabilité conditionnelle, celle de A sachant B, si on connait :
celle de A
celle de B
celle de B sachant A
Définition :
Théorème
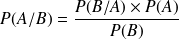
Il peut être facilement retrouvé à partir de la définition des probabilités conditionnelles.
Théorème de Bayes et tests diagnostiques
A partir de ce théorème, on peut calculer la VPP d'un test diagnostique connaissant :
la prévalence de la maladie :
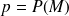
la proportion de tests positifs :
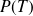
la sensibilité :
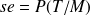
En effet :
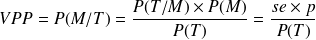
On peut encore décomposer
:
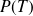Or :
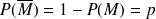et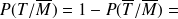
spécificité
Donc :
D'où :
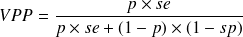
On peut encore écrire la formule précédente :
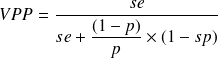
Cette formule montre le lien entre la prévalence p et la VPP. Quand la prévalence augmente, la VPP augmente. On pourrait montrer de la même manière le lien entre prévalence et VPN.
Conséquence
Alors que le sensibilité et la spécificité sont généralement fixes, la VPP et la VPN varie en fonction de la prévalence d'une maladie. Cela signifie qu'un test n'a pas la même valeur d'une région à une autre (par exemple le test diagnostique du paludisme en Afrique et en Europe).
